第二学期初二数学期中诊断测试题
（时间：90分钟 满分：
100分）
填空题（本大题共30分）
直线
在
轴上的截距是________。
一次函数
的值随x的增大而减小，那样
的取值范围是____________。
沿轴向上平移5个单位，得直线的表达式为______________________。
直线
在
轴上方的点的横坐标的取值范围是______________________。
直线
经过1、2、四象限，那样直线
不经过第_______象限。
直线
与直线
平行，并且直线与轴交点到原点的距离是2，则这条直线的分析式为__________________________。
关于的方程
的根是_______________。
方程的根是______________________。
设
，则方程
可化为关于的整式方程是___________________。
假如关于的方程
有增根，则
_______________。
关于的方程
无实数根，
的取值范围是____________________。
假如一个多边形的内角和是外角和的2倍，那样这个多边形的边数是_____________。
菱形的周长为40，两条对角线之比为3：4，则菱形的面积为_________________。
矩形两条对角线相交所成的锐角是，短边长为
，这个矩形的对角线长是______
。
矩形
中，那点到对角线
的距离是_________________。
选择题（本大题共10分）
下列各式是一次函数的是（ ）
下列方程中，有实数解的是（ ）
函数
和函数在同一坐标系中的图像大致是（ ）
下列命题中，真命题的是（ ）
对角线相等的四边形是矩形
对角线互相垂直的四边形是菱形
对角线互相垂直平分的四边形是正方形
对角线互相平分的四边形是平行四边形
某商品的生产流水线每小时生产100件商品，生产前没积压，生产3小时后安排2人装箱，若每小时装150件，未装箱的商品数目y是时间x的函数，那样这个函数的大致图像是（ ）
解方程（本大题共20分）
22.
24.
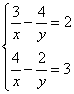
简答卷（本大题共40分）
一次函数图像经过点，且与直线
平行，求一次函数分析式和这个函数图像与两坐标轴围成的三角形的面积。（6分）
一次函数图像经过,与两坐标轴围成的三角形面积是6，求这个函数分析式。(6分）
如图，线段AB、CD分别是一辆轿车的邮箱剩余油量
（升）与另一辆客车的油箱剩余油量
（升）关于行驶路程（千米）的函数图像。
分别求、关于函数分析式，并写出概念域。
假如两车同时出发，轿车的行驶速度为每小时100千米，客车的行驶速度为每小时80千米，当邮箱的剩余油量相同，两车行驶的时间相差几分钟。（8分）
在平行四边形ABCD中，E、F是AB、CD的中点，求证：四边形EHFG是平行四边形。（6分）
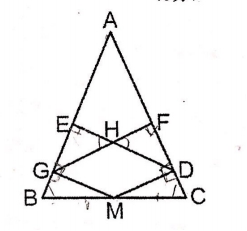
在△ABCD中，AB=AC,BM=CM,MD⊥AC,MG⊥AB,DE⊥AB,GF⊥AC,求证：四边形HGMD是菱形。（6分）
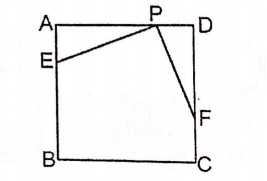
已知正方形ABCD的边长为6，E、F、P分别是AB、CD、AD上的点（均不与正方形顶点重合）且PE=PF,PE⊥PF。（8分）
求证：AE+DF=6
设AE=，五边形EBCFP的面积为，求与的函数关系式，并求出的取值范围。
